一道有趣的几何题，无从下手的感觉

原题如下：

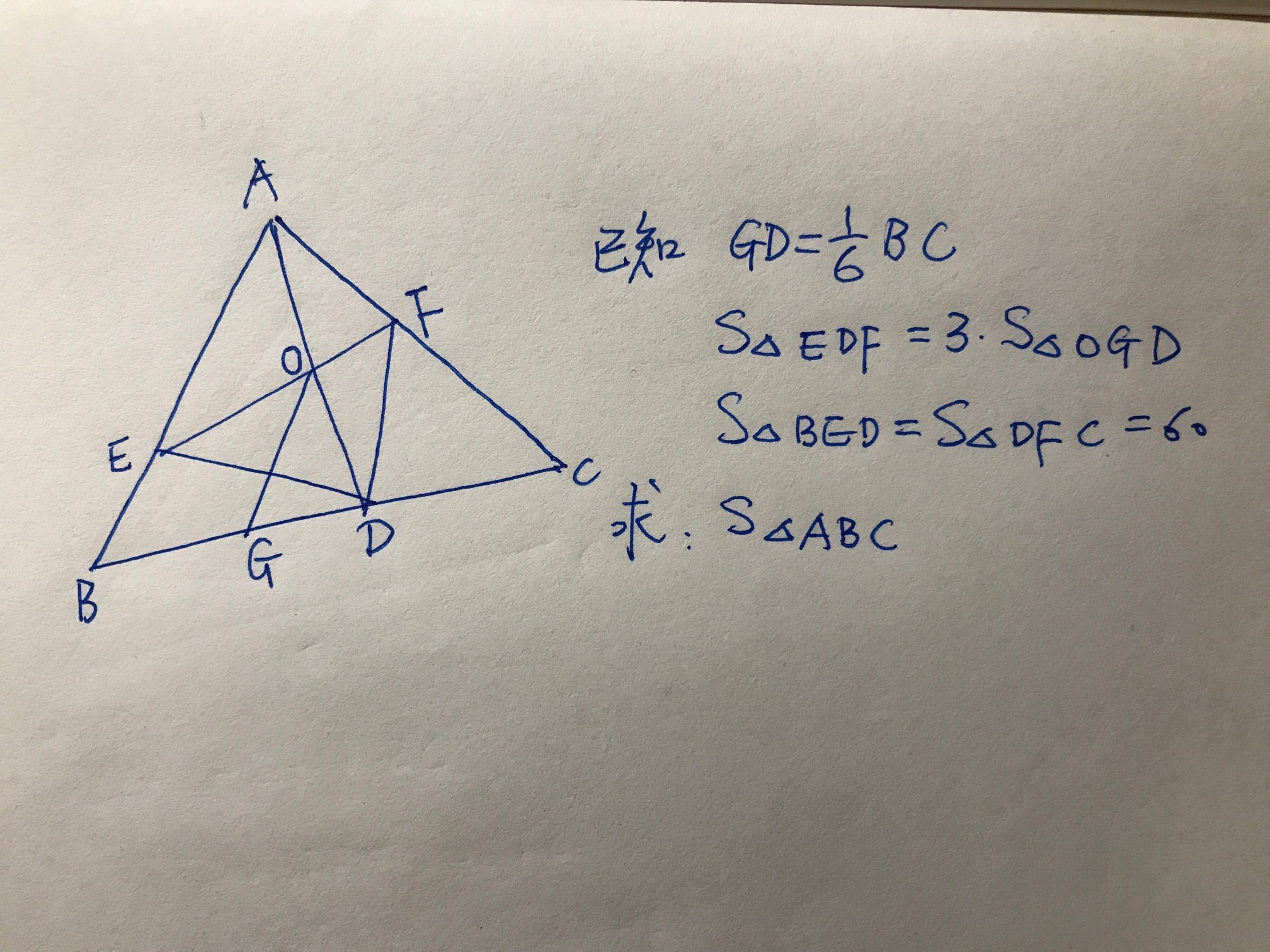
在三角形ABC中，GD=1/6BC，三角形DEF的面积是三角形OGD面积的3倍。

如果三角形BED和三角形DFC面积都是60，那么三角形ABC面积是多少?

///////////////////////////////////////////////////////////

思考20分钟，

找找思路，

试探一下各种能想到的方法

///////////////////////////////////////////////////////////

这道题的难点在不确定。三角形ABC不确定，点DEF也没有固定。

ABC中的几个小三角形即不同同底，也不等高。如何解题呢？

我们知道共底模型中，两个三角形共用一个底边，各自的高不同。

在等高模型中，两个三角形等高，但底不同。

我们需要通过思考，把此题中的已知条件转换为熟悉的模型

然后进行讨论。

如何转换？

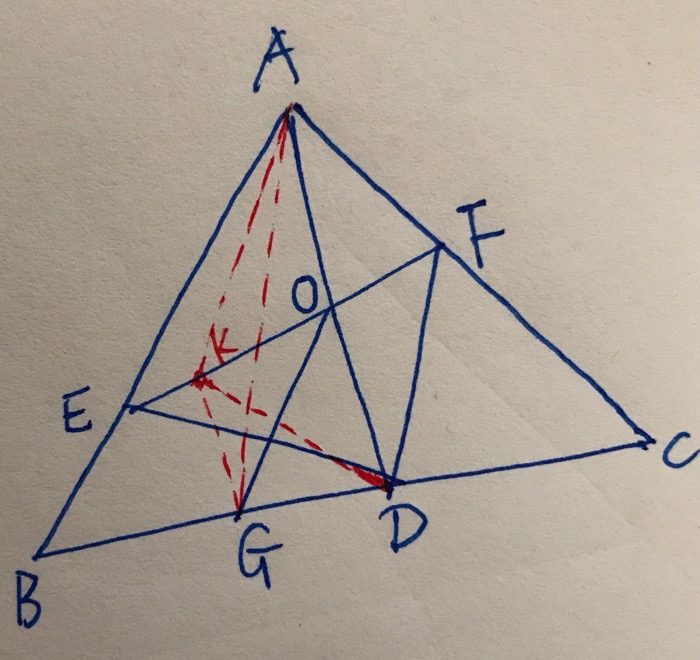
已知，GD=1/6 * BC 

那么，连接AG，▲AGD和▲ABC 可以应用等高模型

已知，▲EDF = 3 * ▲OGD

那么作平行线GK//AD

那么▲OKD = ▲ OGD（等高模型）

那么 KO = 1/3 * EF

连接AK，

那么▲AKO = 1/3* ▲AEF

因为GK//AD

同样有 ▲AKO = ▲AGO

由于▲AGO + ▲ OGD = ▲AGD = 1/6 * ▲ABC

 ▲AGD = 1/3 * 四边形 AEDF

可以知道 四边形 AEDF占▲ABC的1/2

▲ABC的另外1/2 是 ▲BED和▲DFC，各60

所以▲ABC = 240

解毕