原题：学校设置了大量选修课供学生选择，已知某个小组9名同学中，任何3名学生都有两人选同一门课，但每人最多只能选3门课。请说明至少有3人选择了同一门选修课。


请先考虑20分钟……

 
解析：
设9名同学分别是P1、P2…P9，课程分别为C1、C2、C3……
考虑应用反正法，假设一门课最多只有两人报名，如果根据这个假设推导出与原题条件相矛盾的结论，那么也就证明假设存在错误，也就是一门课会有超过2人报名，这样就间接的证明了原题结论，即至少有3人选择同一门课。

根据假设，一门课最多只有两人报名，那么最少有几门课？

课程要最少，自然要求报名的人少，9名学生中，可以有1人报0门，因为如果有2人报0门，那么这两人与其他任何一人组成的3人组不满足“任何3名学生都有两人选同一门课”的条件。剩下8人都需要报课程，两人组合共有28种（8*7/2）。

这28中组合都报了不同的课程，因为如果有两个组合如P1、P2和P3、P4报了相同的课程，那么P1、P2、P3这三人就选择了同一门课了。所以至少有28门课。已知，每人最多只能选3门课，9人最多选27门不同的课，如果是28门课那么只能有同学选的课程大于3门，与原题条件矛盾。
所以，假设错误，也即是至少有3人选择同一门课。


还有一种解释，仍然是反正法，我们假设每门选修课最多2人报名。
对于P1，根据题意他最多选3门课，设为C1、C2、C3，那么他最多只有三个同学P2、P3、P4，假定（P1、P2）选C1，（P1、P3）选C2，（P1、P4）选C3，P1不能有同样选C1或C2或C3课程的第四名同学了，因为如有，直接就满足至少有3人选择同一门课。同样的道理，P5选课程C4、C5、C6，也最多只有三名同学，假设为P6、P7、P8。此时P9与P5、P1的三人组没有任何两人选择的课程相同。与题意不符。假设错误，因此至少有3人选择同一门课。

食堂进行满意度调查，调查分为饭菜口感、饭菜新鲜度、饭菜种类和服务态度共4个方面，每个方面都有非常满意、一般满意和不满意这3个选项。只有对4个方面的内容都做了回馈，且每个方面都只进行单选才算有效问卷。调查收回了若干份有效问卷，结果发现任意3份有效问卷中，都存在1个方面的内容各不相同。问：最多收回了多少份有效问卷？

思考20分钟。。。。

解题思路：

从小规模入手考虑，比如只有1道题的问卷，再考虑只有2道题的问卷。

原题如下：

A、B两位聪明学生分别在两个房间，老师与他们玩一个抛硬币的游戏。

规则如下：

老师在A、B学生房间各抛一次硬币，A猜B房间硬币的正反情况，B

猜A房间硬币的正反情况，只要有一个人猜对，A、B都将同时得到奖品，

如果没有人猜对，则都没有奖品。在抛硬币之前A、B可以交流一次，但之后就不能交流了。

问，A、B是否有一个必胜的策略。

原题如下：
用15块大小是4x1的矩形瓷砖和一块大小是2x2的正方形瓷砖，能否恰好覆盖8x8的正方形地面。

///////////////////////////////////////////////////////////
思考20分钟，
找找思路，
试探一下各种能想到的方法，
看看最远能走到哪里
///////////////////////////////////////////////////////////

解析：
这类问题，从原题中获得数据很少，不能直接进行分析。
可以简单的尝试构造一下，应该会发现覆盖不了。
因此，我们的思路如下：
首先假设能覆盖，那么得到结果A
如果结论A有明显的矛盾点，并不成立，那么我们的假设就是错的，
原题可以得到证明。
如果A没有矛盾点，那么我们给出一个构造方案。

我们把8x8的地面按下面的方式染色，色块总数32，是偶数。
那么4x1的地砖无论怎么摆放，都可以覆盖2个色块和2个白块，
2x2的地砖也一样，都可以覆盖2个色块和2个白块
奇偶性分析没什么问题，这种染色方式不合适。

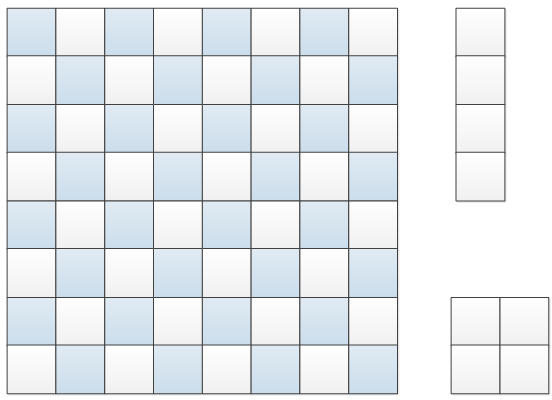
图1

第二种染色方式：
简单变换一下，所有和主对角线平行的方块都间隔染色，那么这样2x2的地砖只能覆盖1个色块或3个色块，不可能是偶数个色块。
4x1的地砖无论如何布置仍然可以覆盖2个色块
此时，如果能完全覆盖，总的色块数是15*2+1或15*2+3，与总的色块数32不一致
所以假设有问题，也即不能完全覆盖。

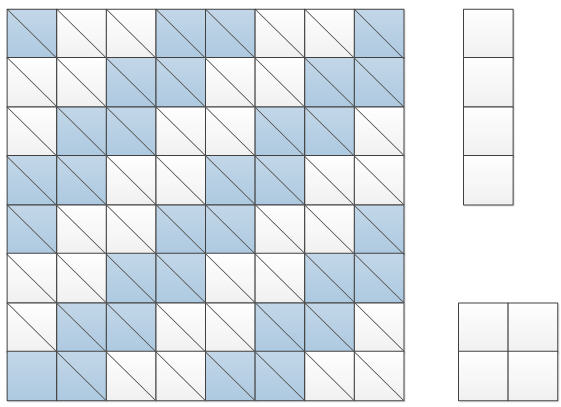
图2

第三种染色方式：
染色的设计目标，让4x1的地砖能覆盖4种颜色，2x2的地砖只能覆盖3种颜色。
如下如，所有主对角线的色块都染成相同的染色，这样2x2的地砖对角线两个颜色也就相同了，所以最多覆盖3种颜色。因为4种染色都间隔着染，4x1的地砖无论如何放都能覆盖4种颜色的一种。
那么，15块4x1的地砖覆盖了各4种颜色块的各15块，剩余4种颜色各1块
但2x2的地砖最多只能覆盖其中3种颜色，无法全部覆盖这4种颜色，所以无法全部覆盖。

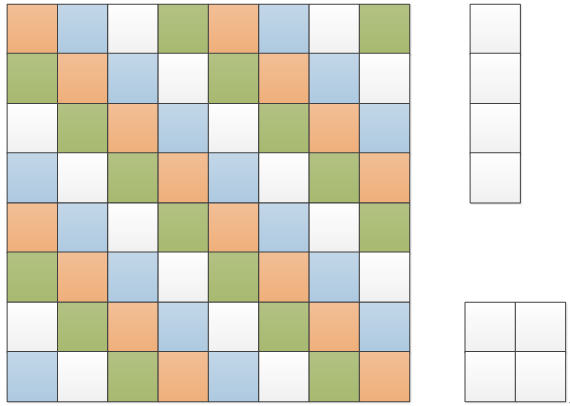
图3

点评：
染色问题是一类与抽屉原理和图论知识联系在一起的数学问题，比如像Ramsey定理“世界上任意6个人中，总有3个人相互认识，或互相皆不认识”就可以用染色法进行分析。

解决方格染色问题的关键是要确定用几种颜色以及用何种方式给方格染色。交替染色方案是比较常用的，但对于有些问题要根据题意用多种染色方式进行试验，从中找出解决问题的正确途径。如果想不到合适的染色方式，就要多做做练习题，看看其他人的解题方案，拓展一下思路，知识积累下来就成为经验，最后也就不怕难题了。

原题如下：

在一个10行10列的棋盘上，任意放入15枚棋子，每个棋格中最多放一个。请证明：可以从其中挑出5行和5列，使所有棋子都在挑出的行或列中。

///////////////////////////////////////////////////////////
思考20分钟，
找找思路，
试探一下各种能想到的方法，
看看最远能走到哪里
///////////////////////////////////////////////////////////

解析：

首先建立画面感，15枚棋子放入棋盘上，一定有一些行有多枚，有些行只有一枚或没有。

挑出5行，要包含尽量多的棋子，自然选棋子最多的5行。

那么考虑棋子最多的5行至少有几枚棋子？这是这道题的突破口。接下来计算论证，这也不容易的。

棋盘总共10行，分成两组，棋子多的5行为一组和棋子少的5行为一组，

并且棋子多的那组每行棋子数不少于棋子少的组每行棋子数。

那么

对于棋子少的那5行，最多总共能有5枚棋子，

因为如果有6枚，按抽屉原理，

必然有一行有2枚或2枚以上棋子。

而多的那一组，因为只有9枚棋子（15-6=9），因此，

必然有1行只有1枚。

这样与我们的假定相矛盾。

所以，对于棋子少的那5行，最多总共能有5枚棋子

也即棋子多的那5行至少有10枚棋子

我们选这5行，

还剩下5枚棋子，用5列去选必定都可以选中。

原题证毕。

点评：

这道题还可以对10行按棋子数进行排序，从多到少，编号为1、2、3、4、。。。直到10

我们讨论第5行。

如果第5行的棋子数<=1，那么后续6、7。。。10行都<=1，选前5行棋子数必然>=10

如果第5行棋子数>=2，那么前5行棋子总数必然>=5*2=10

这么证明似乎更简洁一些，但也要求孩子建立排序讨论的思想。

此题在构造论证的过程中用到了抽屉原理、排序等数学方法，看似简单却是一道锻炼思维的好题。

原题如下：
有n（n≥6）名乒乓球选手进行单循环比赛，比赛结果表明：任意5人中既有1人胜其余4人，又有1人负于其余4人，求证：必有1人胜其余n-1人。

///////////////////////////////////////////////////////////
思考20分钟，
找找思路，
试探一下各种能想到的方法，
看看最远能走到哪里
///////////////////////////////////////////////////////////

解析：
因为n不是一个定数，不能通过直接的分类枚举法来证明。
反正法是一种思路，
我们可以假设：没有人胜其余n-1人
假定，胜场最多那个人的编号是1号，

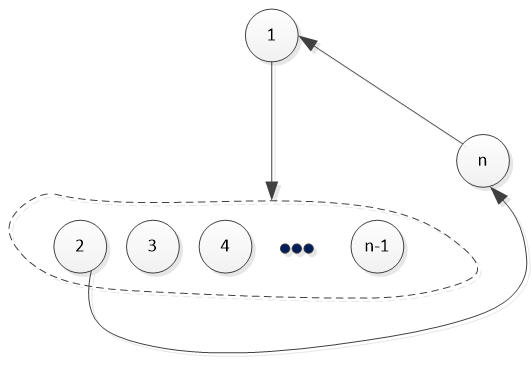
图1

他至少有一人没有胜，设为n，即n打败了1

那么在被1打败的人里面，一定可以找到一个人，比如2号，他打败了n

因为如果没有人能打败n，那么n胜场次就会比1号多1场，与我们的假设矛盾。

所以，此时1、n和2他们的关系是互胜的。

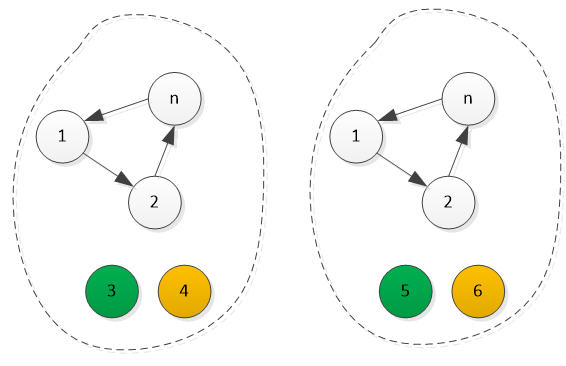
图2

这时我们考虑5人组 1、2、n、3、4

因为1、2、n都有败场，那么全胜的人必定是3或4，我们假定是3全胜，4全败

我们考虑5人组 1、2、n、5、6

那么全胜的人必定是4或5，我们假定是5全胜，6全败

我们考虑5人组 1、2、n、3、5

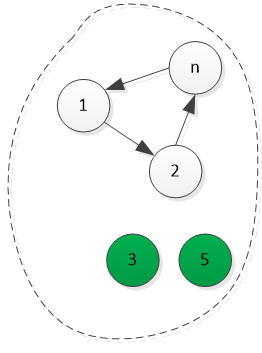
图3

这时我们找不出全败的那个选手，与原题条件矛盾了。
因此我们可以推断，我们的假设错误，
也就间接证明了必有一个人胜其余n-1人。


上面是反正法，我们也可以考虑用直接证明法来试试。
从最小的5个人开始讨论

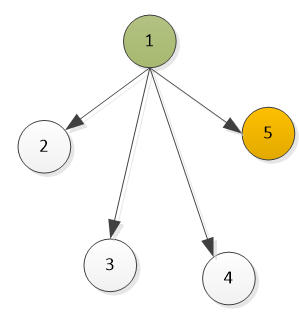
图4

假定有5人，编号为1、2、3、4、5
1胜了其余4人，
现在考虑增加一个6号

讨论1、2、3、4、6这一组
有两种情况：
情况1：如果1胜了6

图5

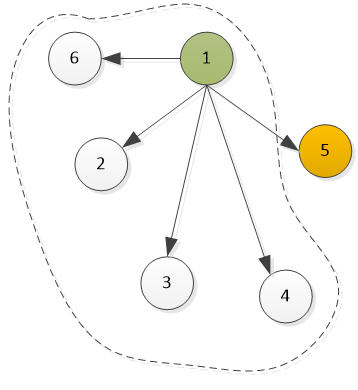
那么1也就胜了2到6的所有人

情况2：如果6胜了1

图6

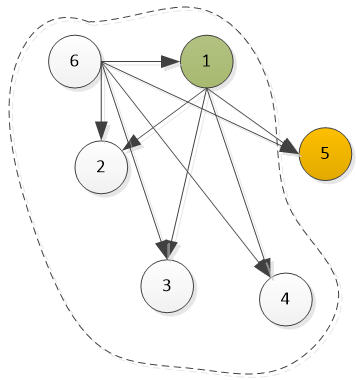
考虑组1、2、3、4、6
因为1胜2、3、4
那么2、3、4不能是全胜的那个，
而1败于6
因此全胜的只能是6号
同样考虑组1、2、3、5、6
6号也必然是全胜的，即6胜5
所以6号胜了所有1到5号

基于上述两种情况的讨论，我们可以找到一个选手（1号或6号），他能全胜。

如果是1号全胜，考虑增加7号，
根据类似的分类讨论，我们也能找到一名全胜的选手，他可能是1号或7号

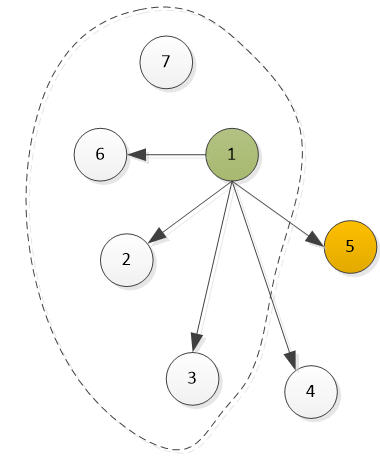
图7

如果是6号全胜，考虑增加7号，
根据类似的分类讨论，我们也能找到一名全胜的选手，他可能是6号或7号

图8

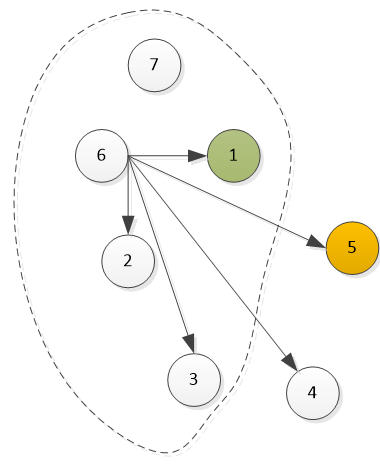
这个过程一直到增加选手n，在他之前，我们可以找到一个选手，胜了所有人，
假定为n-1号

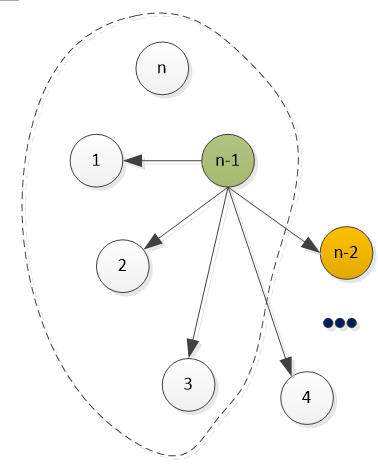
图9

那么n与n-1之间有胜负两种情况：
情况1：n-1胜n，那么n-1就胜了所有人，原题得证
情况2：如果n胜n-1
那么考虑组1、2、3、n-1、n
因为必有1人全胜，1、2、3、n-1都有败场
所以n胜1、2、3
考虑其他组 2、3、4、n-1、n，
同样n胜4
以此类推，n胜n-2
也就是n胜了所有其他人。
原题得证。



点评：
反证法是间接证明，也叫归谬法。在应用的时候，由于多了一个假设，相当于多了个已知条件，自然会好入手一些。但要找出一个并不显而易见的证明仍是一个相当大的智力成就，即便是彻底理解它也需要一定的脑力。

反证法在使用的时候也有一些显而易见的缺点。在聆听或演绎一个证明时，我们不得不自始自终都把我们的注意力集中在一个我们应该要忘记的错误假设上，而不是一条我们应该记住的定理。尤其当反证法这样的证明逻辑很长时，对于听众会很痛苦，我们一个又一个的验证所有的推导过程都正确，但又必须面对全部情况都是不可能的。

对于同一个命题，需要又一点经验才能察觉到直接证明和反证（间接证明）这两者之间并没有本质的对立，两者间也可以进行转化。简而言之，如果我们希望充分的利用自己的能力，就应该熟悉直接和间接两种证明方法，当我们通过一种方法得出一个结论后，也不应该忘记回头再看看这个解答并自问：能否以不同的方式推导出这个结果吗？