原题如下：

有若干把锁，现有6个人各掌握了其中一部分锁的钥匙，已知任意2人同时去开锁，恰好有一把锁打不开，而任意三个人都可以把全部锁打开。那么至少有几把锁。

 

///////////////////////////////////////////////////////////
思考20分钟，
找找思路，
试探一下各种能想到的方法
///////////////////////////////////////////////////////////

 

 

解析：

这道题属于最值问题，需要我们构造论证。

但如果一上来就开始构造，会浪费很多时间。

我们要分析原题带来的限制条件。

设锁为1、2、3、。。。n

6个人分别为P1、P2、P3、P4、P5、P6

 

首先考虑“已知任意2人同时去开锁，恰好有一把锁打不开”。

这里有6个人，任意两人的组合有C(6,2)=15种

在这15种组合中，我们要问一个问题：是否有两种组合它们打不开的锁相同？

如有相同，比如P1+P2和P3+P4都开不了锁1，

那么也就是P1+P2+P3+P4这4个人一起都打不开锁1，

这和原题中第二个条件矛盾了，即“任意三个人都可以把全部锁打开”。

所以，我们可以得到：

这15种组合中，打不开的锁都互不相同

也就是说锁的个数n>=15

 

我们讨论n=15的情况。

假设P1+P2缺第k把钥匙，那么k一定在P3、P4、P5、P6手中，

因为“任意三个人都可以把全部锁打开”

同样，对于任意一把钥匙k，有且只有4个人有。

每把锁有且仅有4把同样的钥匙，

这样我们可以计算每个人有几把钥匙：

15x4/6=10（把）

 

进过上述讨论，我们知道锁有15把，每个人有钥匙10把，我们尝试构造。

我们知道每两个人都缺一把钥匙，可以列表表示如下：

组合	缺钥匙编号
P1+P2	1
P1+P3	2
P1+P4	3
P1+P5	4
P1+P6	5
P2+P3	6
P2+P4	7
P2+P5	8
P2+P6	9
P3+P4	10
P3+P5	11
P3+P6	12
P4+P5	13
P4+P6	14
P5+P6	15

根据以上缺钥匙编号的假定，我们可以构造出每个人拥有钥匙的情况：

组合	缺少钥匙编号	拥有钥匙编号
P1	1、2、3、4、5	6 7 8 9 10 11 12 13 14 15
P2	1、6、7、8、9	2 3 4 5 10 11 12 13 14 15
P3	2、6、10、11、12	1 3 4 5 7 8 9 13 14 15
P4	3、7、10、13、14	1 2 4 5 6 8 9 11 12 15
P5	4、8、11、13、15	1 2 3 5 6 7 9 10 12 14
P6	5、9、12、14、15	1 2 3 4 6 7 8 10 11 13

点评：

本题是需要先证明后构造的逻辑推理题，与前几天的那道连续自然数数码和不是16倍数的那道题刚好相反。这类题是近年以来数学竞赛的热点，要求我们不仅要善于观察和思考，还要敢于猜测和联想。

原题如下：

最多有多少个连续的自然数，它们的各位数字和都不是5的倍数？

 

//////////////////////////////////////////////////

思考过程：

先举一个例子，如

1、2、3、4、5、6、7、8、9、10、11、12、13、14、15

这一串数，它们的各位数字和分别为：

1、2、3、4、5、6、7、8、9、1、2、3、4、5、6

因为，这些数要求是连续的自然数，那么后一个自然数一定比在它前面的自然数大1

如果它们除了个位数以外的数字都相同，那么它们的数字和也将是一些相邻的自然数，

比如这里的

10、11、12、13、14、16

它们的十位相同仅个位数不同，其各位数字和分别是：

1、2、3、4、5、6

是一串连续的自然数。

数串8、9、10、11、12就不符合这个规律，因为它们十位不同。

 

我们还知道，

任何连续的5个自然数必然有一个能被5整除

因为5各连续自然数除以5的余数只能有1、2、3、4和0 这5种情况

 

考虑原题的要求，我们猜测：

仅个位数不同的自然数串最多连续有4个，其数码和不是5的倍数

另外在加上十位数与上述不同的连续4个，

总共是8个

比如 6、7、8、9、10、11、12、13

 

对于上述猜想，我们需要严格证明。

要证明最多是8个，自然想到9个可不可以，或者比8个多是否可行？这是反证法，也就是归谬法。如果超过8个不可以，同时我们又能构造出8个连续自然数的一个例子，那么也就完成了证明。思路是这样，考虑如何入手。

 

设有一串自然数，个数大于等于9个。根据前面的讨论，我们知道

1、如果它们除了个位数以外的数字都相同，那么它们的数字和也将是一些相邻的自然数

2、任何连续的5个自然数必然有一个能被5整除

能想到什么？这9个数有可能除了个位数以外的数字都相同，也有可能十位数不同。

按照十位数以上数字是否相同，我们把这9个数分为两类，根据抽屉原理，必然有一类数字个数大于等于5个，那么这5个数，它们的各位数码和就是连续的5个自然数，也就是有必能被5整除的一个数。

 

这样就证明了前面的猜想。

所以本题的答案是8

 

 

这类问题，还有升级版，题目如下：

最多有多少个连续的自然数，它们的各位数字和都不是16的倍数？

 

解析：

最小的两位数79其数字和等于16，也就是从1开始直到78，

这78个自然数其数码和都不是16的倍数。

那么78是最多的满足条件的连续自然数个数吗？

 

类似第一道题的考虑方式，按百位以上数字是否相同我们把目标的这串数分为两段，

后一段从1000….00（K个0），开始直到1000…0068（K个0），

最后两位数字不能超过68，因为1+6+9=16了

前一段应该从999….开始到999…99（K个9）

 

接着分析，

00、01、02直到68，这两位数码和是0到14，共15个，没有其他了

从31、32、33直到99，这两位数码和是4到18，共15个，也没有其它了

这样最好了，我们目标就要构造这样的数列。

因为如果有16个数码和，则必然有一个能被16整除（抽屉原理）

继续构造第一个数99..31

31前面有n个9

目标：9*n + 4除16余1

n=5满足

即9999931直到9999999这69个数的数码和除16的余数只能是1到15之间的任意数，

不会有数的数码和被16整除

 

所以9999931到10000068这138个数的数码和不能被16整除。

 

是否138就是最大呢？

这里的证明需要用到抽屉原理，

即把大于等于139个连续的自然数，按百位以上数码是否相同分成两部分，其中一部分必然大于等于70个。

假设：

1、大于70个数的那一组最大的百十位数为99

那么这一组最小数必然小于等于30，

其数码和从3到18，共16个，包括16，根据抽屉原理

不论其百位以上数码和是多少，这一组数中必有一个数的数码和能被16整除。

 

2、大于70个数的那一组最小的百十位数位00

那么这一组最大数必然大于等于69，

其数码和从0到15，共16个，包括16，根据抽屉原理

不论其百位以上数码和是多少，这一组数中必有一个数的数码和能被16整除。

 

也就是说，138是最大的自然数数串的数字个数。

点评：

第一题虽然简单，其实我们也用了构造。从简单的数列构造中，探寻约束条件下的规律。

第二题，如果没有构造目标数列，我们不能直接想到70个连续自然数的数串的性质，也就不能应用抽屉原理来进一步证明。在构造的过程中，我们也应用了抽屉原理。抽屉原理本身也是一种抽象的构造技巧，即我们要设计抽屉，也要设计苹果。

在解题的很多时候，我们要经常想一想，是否有做过类似的题，这个难题的简化版本是什么。

从简单入手，套用熟悉的模型，往往是一个解决复杂问题的有效办法。

甲乙两个人手上各有一些牌，具体如下：
甲： 一对A  一对10 
乙:  红心 3 、5 、9 、Q 、2
     黑桃  4 、6  、7 、J 、Q 
     梅花  4 、6 、9 、J 
     方片  5 、7 、J 、Q

规则：
不许出连对、三个不可以带牌 
可以出顺子、同花（5张同色一起出）
谁先出完谁胜

乙先出，乙是否能赢？

///////////////////////////////////////////////////////////

对于乙，

黑桃的5张可以出同花，

红心3、5，梅花4、6方片7可以出顺子

剩下，5、2，99 JJ和QQ

这个时候，出方片5

如果：

1、甲不要，乙则继续打单，直到全部出完

2、甲要，出10

乙出J，

甲出A，那么乙出2，乙还有两个对一个J，继续出完，乙赢

甲不出A，乙继续出单个J，甲继续不出，乙出单个Q，

甲还是不能出A，因为出A后，甲剩下10、A，乙剩下2、99、Q，乙能出完

最后甲两个A只能拿在手里憋死了。

结论是乙可以赢

原题如下：

一个60x100的长方形，全部由1x1的小正方形组成，从长方形的一个角到其对角划一条直线，问，这条直线穿过了多少个正方形。穿过的定义是指直线从正方形内部穿过。如下图这样。

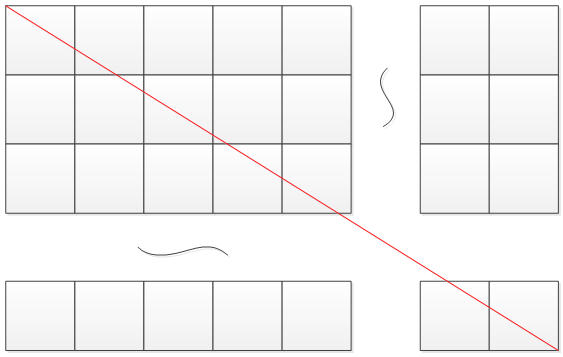
解析：

求直线穿过正方形的数量，我们不要画出来去数，这样很费时间，对建立解题思路也没有什么启发性。

先想想一个简单的问题：

直线穿过1个正方形，会有几个交点。

必然有2个交点，因为如果只有1个交点，就是擦边而过，不是穿过。如有3个交点，那不是直线能做的事。

那么反过来考虑，根据交点数是否可以计算出穿过的正方形数。

 

像下面这个例子，红色的对角线穿过了2条垂直线，1条水平线，总共有3个交点

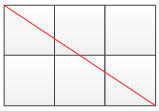
中间这些交点属于两个相邻的正方形共有，在统计时我们要*2

那么加上两个顶角的交点，

2+3*2=8

穿过的正方形数：

8/2=4

 

如果是这种情况，直线穿过了一个小正方形的顶点

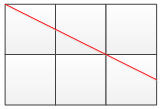
红色的对角线穿过了2条垂直线，1条水平线，总共有3个交点

但其中有两个交点重叠了（即正方形顶点），在统计时需要减去

内部总共的交点数：

3-1=2

穿过的正方形数：

（2+2*2）/2=3

 

这种思路应该是可以的。

也可这么想，数数看直线被分成几段了，这个跟穿过正方形数是一样的。

我们这次决定尝试一下数交点数的方法。

60X100的长方形，内部总共有99条垂线和59条横线，

对角的直线都会穿过这些垂线、横线

总共交点有 99 + 59个

注意，这里面有没有小正方形的顶点？

假设最左上角的顶点为（0，0），最右下角顶点编号为（60，100）

这些编号的顶点都会被直线穿过（只考虑长方形内部）

（3，5）（6，10）（9，15）。。。直到（57，95）

总共有19个点

所以内部的交点 99 + 59 – 19 =139个

那19个顶点重复统计了2次。

穿过的正方形数有

（2+139*2）/2 = 140 （个）

解毕

点评：

对于无法入手的问题，我们可以尝试把问题简化为一个规模不那么大的情形，进行分析和探讨，或者回想一下，是否有做过类似的问题，从简单入手，找出方案。进一步推而广之，向目标问题靠近。

这道题还有几个相对复杂的升级版本，一起来看看。

问题1：

一个10x10x10的大正方体，由1000个单位为1的小正方体组成，一个钢丝从正方体一面穿入从另一面穿出，问，最多能穿过多少个小正方体。

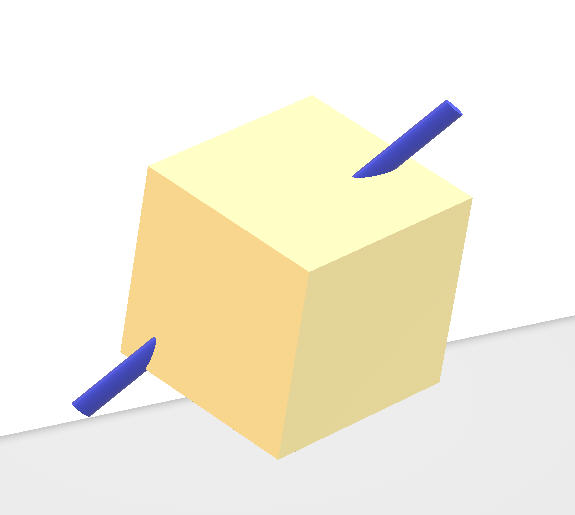
解析：

直线每穿过一个小正方体，最多穿过其两个不同的面，如果从棱线或顶角穿入穿出，那么会相应减少所穿过的面的数量。

为简化问题，我们假设直线全部从面上穿过，即不经过棱或顶点。

那么在正方体内部直线穿过的面有：

前后共9个，左右共9个，上下共9个

一共27个，这些面为两个小正方体共有，在统计时要*2

加上外部的2个面（一进一出）

穿过小正方体最多有（每个小正方体提供2个面）：

（27*2+2）/2=28个

问题2：

小长方体尺寸为1*2*3，共有36块小长方体组成一个6*6*6的大正方体，如下图，问：其对角线CE穿过了几个小长方体。

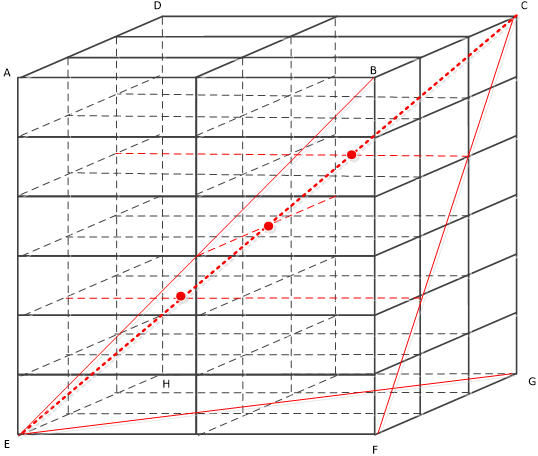
解析：

这道问题更复杂一点，它规定了直线的路径，我们必须要考虑内部是否穿过长方体的棱边，或者顶点。可是对角线在正方体内部，不像上面的题，可以在平面上把图形画出来讨论。我们要通过想象力，建立立体模型，这是这道题的难点所在。

 

先考虑CE这条线在哪几个切面上？这里切面指把正方体切开后展示出来的面。

CE在这几个面上：

DCEF、EBCH、ACGE

而不在DBFH上

如果CE所在的切面穿过了长方体的棱线，那么CE也必然穿过此棱线。

关于上面这一点，不那么显而易见，但仔细考虑后应该能明白。

 

现在来进行计算。

对角线CE穿过的面有：

前后2个，上下5个，左右1个，共8个

考虑内部穿过的棱线有3条（具体如图示），

穿过一条棱，等价于同时穿过了两个面，

穿过一个顶角，等价于同时穿过了三个面（这里没有穿过顶角的情况）

在统计面时应该减掉过棱的次数，所以穿过的小长方体数有：

（（2+5+1-3）*2+2）/2 =6个

如果我们第一次碰到的就是最后这一道题，不一定能分析出结论。

但是，如果我们从最简单的平面分析开始，

一步一步往下走，走到最后的结论应该不难，至少是有考虑的方向了。

这应该就是我们常说的数学解题思维吧。

题目如下：

小明带着小狗一起去上学，从家里一起出发，小狗跑的块，小明走的慢，小狗到了学校门口后又返回去找小明，等碰到小明之后又掉头朝学校跑，一直这么跑直到小明到学校。已知小明家到学校距离1000米，小明每分钟走100米，小狗每分钟走200米，问这个过程中小狗总共走了多少米。

这道题当时在我听来非常新鲜，小狗的跑动行程每一段是动态变化的，而且看似有很多很多个来回，直觉判断此题肯定不是每一段每一段这么算的。那么从哪入手？我们要求路程，因为

路程 = 速度 * 时间

速度我们知道了，只需要知道时间。

那么时间是多少？小狗跑动的时间和小明的时间是否相同？

想到这里，此题应该能解了。

这是一道行程问题非常有趣的拓展题，可以激发孩子对数学兴趣，我当年就是这样的一种体会。