原题：学校设置了大量选修课供学生选择，已知某个小组9名同学中，任何3名学生都有两人选同一门课，但每人最多只能选3门课。请说明至少有3人选择了同一门选修课。


请先考虑20分钟……

 
解析：
设9名同学分别是P1、P2…P9，课程分别为C1、C2、C3……
考虑应用反正法，假设一门课最多只有两人报名，如果根据这个假设推导出与原题条件相矛盾的结论，那么也就证明假设存在错误，也就是一门课会有超过2人报名，这样就间接的证明了原题结论，即至少有3人选择同一门课。

根据假设，一门课最多只有两人报名，那么最少有几门课？

课程要最少，自然要求报名的人少，9名学生中，可以有1人报0门，因为如果有2人报0门，那么这两人与其他任何一人组成的3人组不满足“任何3名学生都有两人选同一门课”的条件。剩下8人都需要报课程，两人组合共有28种（8*7/2）。

这28中组合都报了不同的课程，因为如果有两个组合如P1、P2和P3、P4报了相同的课程，那么P1、P2、P3这三人就选择了同一门课了。所以至少有28门课。已知，每人最多只能选3门课，9人最多选27门不同的课，如果是28门课那么只能有同学选的课程大于3门，与原题条件矛盾。
所以，假设错误，也即是至少有3人选择同一门课。


还有一种解释，仍然是反正法，我们假设每门选修课最多2人报名。
对于P1，根据题意他最多选3门课，设为C1、C2、C3，那么他最多只有三个同学P2、P3、P4，假定（P1、P2）选C1，（P1、P3）选C2，（P1、P4）选C3，P1不能有同样选C1或C2或C3课程的第四名同学了，因为如有，直接就满足至少有3人选择同一门课。同样的道理，P5选课程C4、C5、C6，也最多只有三名同学，假设为P6、P7、P8。此时P9与P5、P1的三人组没有任何两人选择的课程相同。与题意不符。假设错误，因此至少有3人选择同一门课。

食堂进行满意度调查，调查分为饭菜口感、饭菜新鲜度、饭菜种类和服务态度共4个方面，每个方面都有非常满意、一般满意和不满意这3个选项。只有对4个方面的内容都做了回馈，且每个方面都只进行单选才算有效问卷。调查收回了若干份有效问卷，结果发现任意3份有效问卷中，都存在1个方面的内容各不相同。问：最多收回了多少份有效问卷？

思考20分钟。。。。

解题思路：

从小规模入手考虑，比如只有1道题的问卷，再考虑只有2道题的问卷。

没什么好的思路，简单写一个程序，运算结果为36418.5

#!/usr/bin/env ruby
#求算式的和
#sum =  100/(1+0+0)+101/(1+0+1)+102/(1+0+2)+...+998/(9+9+8)+999/(9+9+9)
#the result is: 36418.5
sum = 0
(100..999).each do |i|
  b = 0
  c = 0
  #求出每个数i的数字和，比如100数字和是1,101数字和是2
  #把数字和存到符号b中
  i.to_s.split("").each {|k| b+=k.to_i}
  #求出i/其数字和b，结果存到符号c中
  c = i.to_f/b.to_f
  #把每个i的运算结果求和，保存到sum中，sum是全局变量，可以在循环外部引用
  sum += c
end
puts ">>>>>>>>>>>>>>>>the result is: #{sum}"

原题如下：

A、B两位聪明学生分别在两个房间，老师与他们玩一个抛硬币的游戏。

规则如下：

老师在A、B学生房间各抛一次硬币，A猜B房间硬币的正反情况，B

猜A房间硬币的正反情况，只要有一个人猜对，A、B都将同时得到奖品，

如果没有人猜对，则都没有奖品。在抛硬币之前A、B可以交流一次，但之后就不能交流了。

问，A、B是否有一个必胜的策略。

这是一道18年迎春杯小高组的计算题，我认为很难，太为难小朋友了吧。

原题如下：

20182018...2018（共18个2018）x151514141313...0707的计算结果有多少个奇数数字。

解析：

数字小可以直接算，对于原题这个思路就直接放弃。

那么分析两个数，

20182018...2018（共18个2018） = 2018*00010001...0001（18组0001）

设 151514141313...0707 = S1

S1的数字和为90，那么S1能被9整除

S1的奇数位数字和减去偶数位数字和是66，S1能被11整除

通过观察S1能被101整除，因为S1符合截取两位数的判定方法，即：

一个多位数，截取末两位，由末两位和之前的高位，各形成一个新数，这两个新数相减，
重复上述步骤，直至差足够小，这个差能被101整除，则原数能被101整除。

所以S1能被 9 * 11*101=9999整除

设 S1 = 9999 * S2（S2是1开头的32位数）

那么，

原式 = 2018*00010001...0001（18组0001）* 9999 * S2

=2018*00010001...0001（18组0001） * 9999 * S2

=9999（72个9）*S2

=9999（72个9）*S2*2018

设 S2*2018 = S3，S3应该有35位（因为S2是1开头的32位数）

故原式 = 9999（72个9）*S3（35位数）

分析到这一步，原式已被大大的化简，离最后的结果还有一步。

一般我们做某个数N*999，会改为N*（1000-1）来做

这里也用这个思路试试：

原式 = 【1000...0（72个0）-1】*S3

=S3*1000..0（72个0）-S3

=（S3-1）99...9（99...9-S3+1）【这是减法借位之后的结果描述】

第一部分S3-1是35位的一个数

中间部分999..9有37位（因为原来有72个0）

最后一部分99..9-S3+1仍然是一个35位数

可以看到，第一部分和最后一部分的和恰好是999..9（共35位9），那么

我们可以判断第一部分和最后一部分的奇偶位是互补的，

举个例子：

S3=728

728-1 = 727 和 999-728+1 = 272

9是奇数，必然是一个奇数加一个偶数得到，所以

727和272奇偶位互补，

连起来的这个数字727272奇数位和偶数位数量相同

所以原式=（S3-1）99...9（99...9-S3+1）

有奇数数字35+37=72个，偶数数字35个，总位数107位

补：

我们可以进一步猜测：

 999...9（N个9）*S1（M位数），只要M<N那么结果就有N个奇数

这个猜测的证明与上面过程类似，留给小朋友们作为作业吧。

原题如下：
用15块大小是4x1的矩形瓷砖和一块大小是2x2的正方形瓷砖，能否恰好覆盖8x8的正方形地面。

///////////////////////////////////////////////////////////
思考20分钟，
找找思路，
试探一下各种能想到的方法，
看看最远能走到哪里
///////////////////////////////////////////////////////////

解析：
这类问题，从原题中获得数据很少，不能直接进行分析。
可以简单的尝试构造一下，应该会发现覆盖不了。
因此，我们的思路如下：
首先假设能覆盖，那么得到结果A
如果结论A有明显的矛盾点，并不成立，那么我们的假设就是错的，
原题可以得到证明。
如果A没有矛盾点，那么我们给出一个构造方案。

我们把8x8的地面按下面的方式染色，色块总数32，是偶数。
那么4x1的地砖无论怎么摆放，都可以覆盖2个色块和2个白块，
2x2的地砖也一样，都可以覆盖2个色块和2个白块
奇偶性分析没什么问题，这种染色方式不合适。

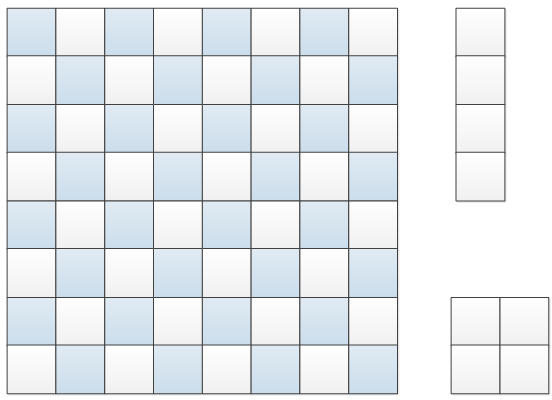
图1

第二种染色方式：
简单变换一下，所有和主对角线平行的方块都间隔染色，那么这样2x2的地砖只能覆盖1个色块或3个色块，不可能是偶数个色块。
4x1的地砖无论如何布置仍然可以覆盖2个色块
此时，如果能完全覆盖，总的色块数是15*2+1或15*2+3，与总的色块数32不一致
所以假设有问题，也即不能完全覆盖。

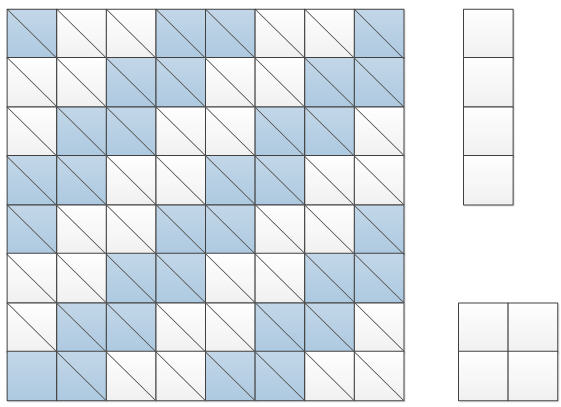
图2

第三种染色方式：
染色的设计目标，让4x1的地砖能覆盖4种颜色，2x2的地砖只能覆盖3种颜色。
如下如，所有主对角线的色块都染成相同的染色，这样2x2的地砖对角线两个颜色也就相同了，所以最多覆盖3种颜色。因为4种染色都间隔着染，4x1的地砖无论如何放都能覆盖4种颜色的一种。
那么，15块4x1的地砖覆盖了各4种颜色块的各15块，剩余4种颜色各1块
但2x2的地砖最多只能覆盖其中3种颜色，无法全部覆盖这4种颜色，所以无法全部覆盖。

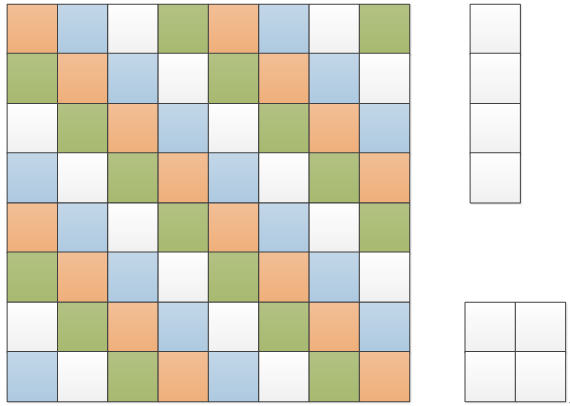
图3

点评：
染色问题是一类与抽屉原理和图论知识联系在一起的数学问题，比如像Ramsey定理“世界上任意6个人中，总有3个人相互认识，或互相皆不认识”就可以用染色法进行分析。

解决方格染色问题的关键是要确定用几种颜色以及用何种方式给方格染色。交替染色方案是比较常用的，但对于有些问题要根据题意用多种染色方式进行试验，从中找出解决问题的正确途径。如果想不到合适的染色方式，就要多做做练习题，看看其他人的解题方案，拓展一下思路，知识积累下来就成为经验，最后也就不怕难题了。