一道关于染色问题的好题，15块大小是4x1的矩形瓷砖。。。

原题如下：
用15块大小是4x1的矩形瓷砖和一块大小是2x2的正方形瓷砖，能否恰好覆盖8x8的正方形地面。

///////////////////////////////////////////////////////////
思考20分钟，
找找思路，
试探一下各种能想到的方法，
看看最远能走到哪里
///////////////////////////////////////////////////////////

解析：
这类问题，从原题中获得数据很少，不能直接进行分析。
可以简单的尝试构造一下，应该会发现覆盖不了。
因此，我们的思路如下：
首先假设能覆盖，那么得到结果A
如果结论A有明显的矛盾点，并不成立，那么我们的假设就是错的，
原题可以得到证明。
如果A没有矛盾点，那么我们给出一个构造方案。

我们把8x8的地面按下面的方式染色，色块总数32，是偶数。
那么4x1的地砖无论怎么摆放，都可以覆盖2个色块和2个白块，
2x2的地砖也一样，都可以覆盖2个色块和2个白块
奇偶性分析没什么问题，这种染色方式不合适。

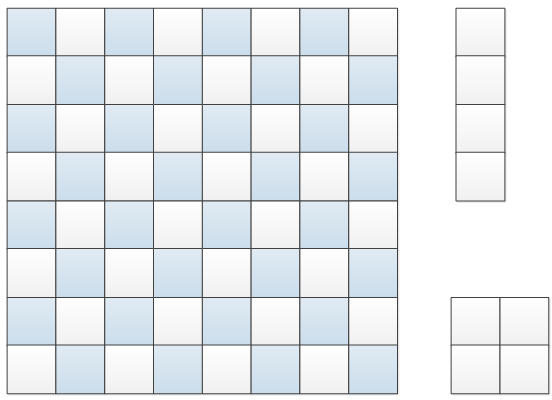
图1

第二种染色方式：
简单变换一下，所有和主对角线平行的方块都间隔染色，那么这样2x2的地砖只能覆盖1个色块或3个色块，不可能是偶数个色块。
4x1的地砖无论如何布置仍然可以覆盖2个色块
此时，如果能完全覆盖，总的色块数是15*2+1或15*2+3，与总的色块数32不一致
所以假设有问题，也即不能完全覆盖。

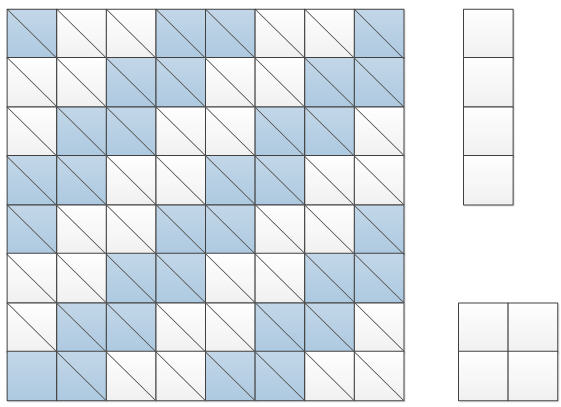
图2

第三种染色方式：
染色的设计目标，让4x1的地砖能覆盖4种颜色，2x2的地砖只能覆盖3种颜色。
如下如，所有主对角线的色块都染成相同的染色，这样2x2的地砖对角线两个颜色也就相同了，所以最多覆盖3种颜色。因为4种染色都间隔着染，4x1的地砖无论如何放都能覆盖4种颜色的一种。
那么，15块4x1的地砖覆盖了各4种颜色块的各15块，剩余4种颜色各1块
但2x2的地砖最多只能覆盖其中3种颜色，无法全部覆盖这4种颜色，所以无法全部覆盖。

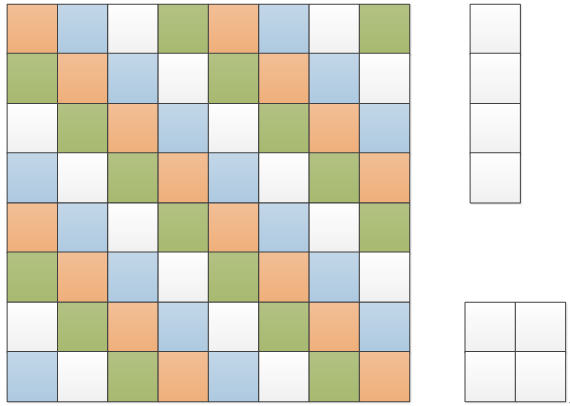
图3

点评：
染色问题是一类与抽屉原理和图论知识联系在一起的数学问题，比如像Ramsey定理“世界上任意6个人中，总有3个人相互认识，或互相皆不认识”就可以用染色法进行分析。

解决方格染色问题的关键是要确定用几种颜色以及用何种方式给方格染色。交替染色方案是比较常用的，但对于有些问题要根据题意用多种染色方式进行试验，从中找出解决问题的正确途径。如果想不到合适的染色方式，就要多做做练习题，看看其他人的解题方案，拓展一下思路，知识积累下来就成为经验，最后也就不怕难题了。