【5星难度】某届IMO试题,很早以前的了,4444的4444次方。。。
2020/09/23
原题如下:
4444的4444次方,其得数记为X,X的各位数字之和记为A,A的各 位数字之和记为B,那么B的各位数字之和为多少?
///////////////////////////////////////////////////////////
思考20分钟,
找找思路,
试探一下各种能想到的方法
///////////////////////////////////////////////////////////
解法如下:
说到数码和,我们自然想一个数到被3整数、被9整除的性质,
即各个数码之和能被3或9整除,那么此数就能被3或9整除。
我们考虑4444除3的余数,余1
那么 4444^4444除3的余数也是1(这里应用了带余数乘法的性质)
也就是
X = 4444^4444 = 1 (mod 3)
A是X的数码和,B是A的数码和,
设C是B的数码和,我们要求C的值
自然
C = B = A = 1 (mod 3)
第二步,考虑A的最大值
X的位数最多 4444*4 = 17776位
所以A < 17776*9 = 159984
A是一个不超过6位的数
B < 6*9 = 54
所以B最多两位
因此C < 5+9 = 14
小于14且除3余1的数有很多,1、4、7、10、13等
确定不了
第三步,我们用模9试试
C = B = A = 7 (mod 9)
C < 5+9 = 14
那么C只能等于7
原题的答案为7
解毕
一道行程问题,小时候舅舅讲给我听的
2020/09/23
题目如下:
小明带着小狗一起去上学,从家里一起出发,小狗跑的块,小明走的慢,小狗到了学校门口后又返回去找小明,等碰到小明之后又掉头朝学校跑,一直这么跑直到小明到学校。已知小明家到学校距离1000米,小明每分钟走100米,小狗每分钟走200米,问这个过程中小狗总共走了多少米。
这道题当时在我听来非常新鲜,小狗的跑动行程每一段是动态变化的,而且看似有很多很多个来回,直觉判断此题肯定不是每一段每一段这么算的。那么从哪入手?我们要求路程,因为
路程 = 速度 * 时间
速度我们知道了,只需要知道时间。
那么时间是多少?小狗跑动的时间和小明的时间是否相同?
想到这里,此题应该能解了。
这是一道行程问题非常有趣的拓展题,可以激发孩子对数学兴趣,我当年就是这样的一种体会。
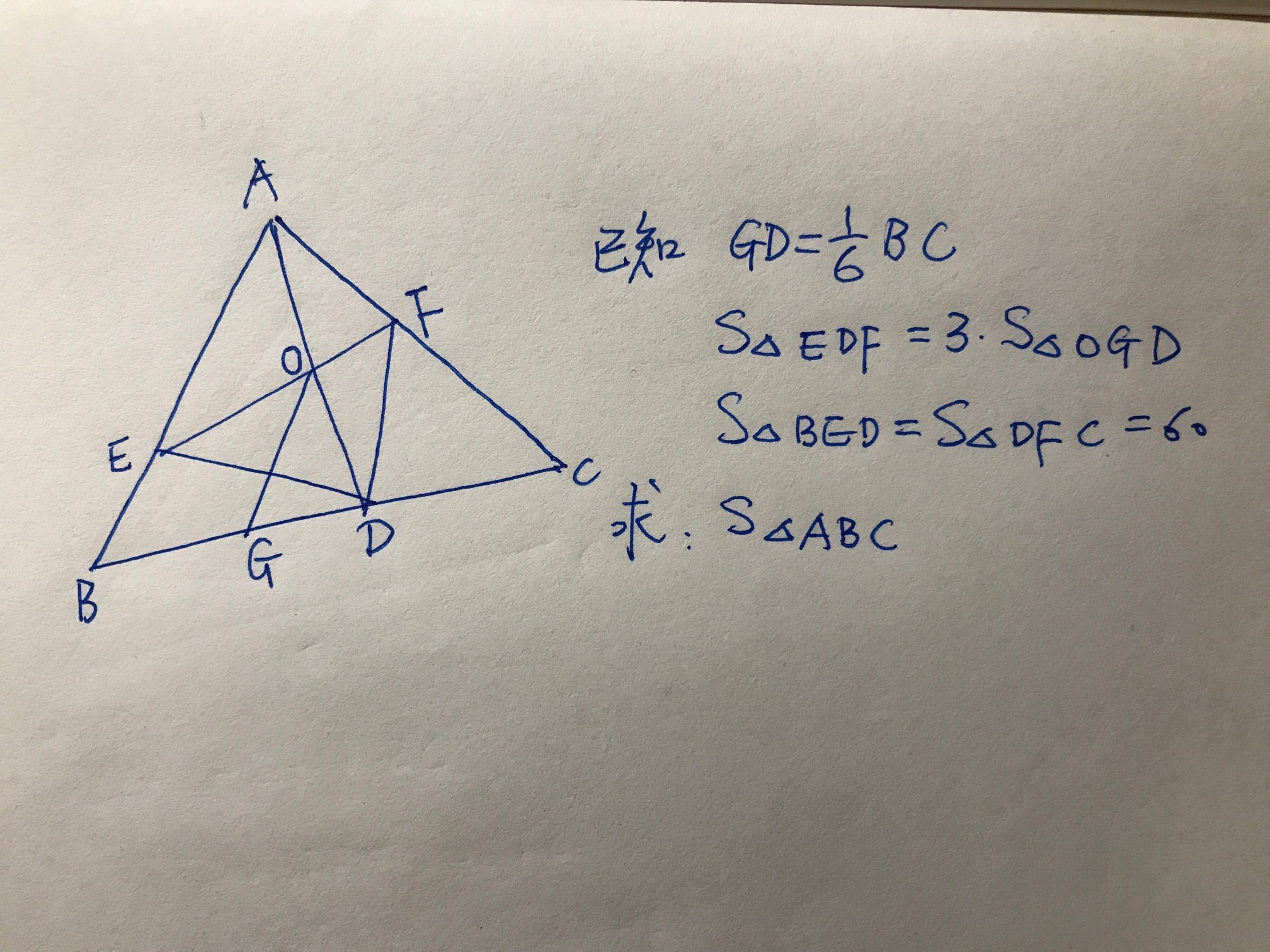
一道有趣的几何题,无从下手的感觉
2020/09/18
原题如下:
在三角形ABC中,GD=1/6BC,三角形DEF的面积是三角形OGD面积的3倍。
如果三角形BED和三角形DFC面积都是60,那么三角形ABC面积是多少?
///////////////////////////////////////////////////////////
思考20分钟,
找找思路,
试探一下各种能想到的方法
///////////////////////////////////////////////////////////
这道题的难点在不确定。三角形ABC不确定,点DEF也没有固定。
ABC中的几个小三角形即不同同底,也不等高。如何解题呢?
我们知道共底模型中,两个三角形共用一个底边,各自的高不同。
在等高模型中,两个三角形等高,但底不同。
我们需要通过思考,把此题中的已知条件转换为熟悉的模型
然后进行讨论。
如何转换?
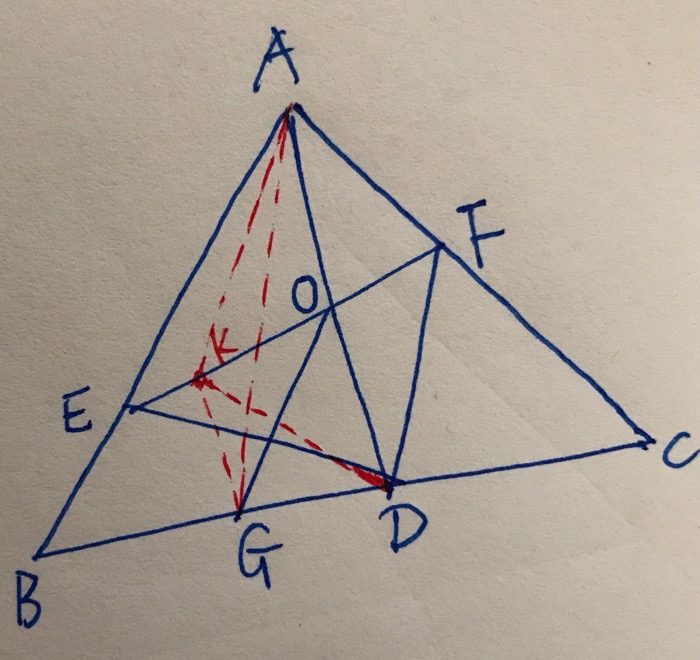
已知,GD=1/6 * BC
那么,连接AG,▲AGD和▲ABC 可以应用等高模型
已知,▲EDF = 3 * ▲OGD
那么作平行线GK//AD
那么▲OKD = ▲ OGD(等高模型)
那么 KO = 1/3 * EF
连接AK,
那么▲AKO = 1/3* ▲AEF
因为GK//AD
同样有 ▲AKO = ▲AGO
由于▲AGO + ▲ OGD = ▲AGD = 1/6 * ▲ABC
▲AGD = 1/3 * 四边形 AEDF
可以知道 四边形 AEDF占▲ABC的1/2
▲ABC的另外1/2 是 ▲BED和▲DFC,各60
所以▲ABC = 240
解毕
【4星难度】一道应用缩放法的计算题19*(1/10^2+1/11^。。。+1/2014^2)
2020/09/12
原题如下:
求 19 * (1/10^2+1/11^2+1/12^2+...+1/2013^2+1/2014^2)的结果整数部分。
10^2表示10的2次方
///////////////////////////////////////////////////////////
先自行思考20分钟,
找找思路,
试探一下各种方法
///////////////////////////////////////////////////////////
这类问题硬着头皮算是不可行了,除非用计算机写个小程序。但在考场上,应该也不方便写程序了。
所以必须考虑其他方法。
这是个估值问题,不需要计算准确结果。估值就自然想到缩放法,即找值的上限和下限
比如,设原式的值为P,我们有 P>0,也容易得到 P<19*0.01*2005<381(把每个分数都看成1/10^2,共2005个分数)
那如何找出更小的界限?
我们从单个分数入手
1/10^2=1/(10*10)=1/100
针对1/100,最小的估值界限我们有:
1/101<1/100<1/99
同样,1/11^2
1/122<1/121<1/120
以此类推,这样问题就转化为求 1/101+1/122+1/145 +。。。+Last的和,这是最小值。
这些分数之间并没有什么计算模式可以联系,让求和过程变得简单。
这个思路不是很理想,必须换一换。
这次我们对缩放以后的分数数列要能够方便求和的角度出发重新进行考虑,
分数数列求和有一种模式是前后能销项,如:
1/2*3+1/3*4+1/4*5=1/2-1/3+1/3-1/4+1/4-1/5=1/2-1/5
这种模式和原题应该有某种联系,这是我们灵感一闪的时刻 :)
缩放法相比普通计算题更有创新性和挑战性,我们可以自己设计缩放的模式。
这次这样来设计:
1/(10*11)<1/(10*10)<1/(9*10)
1/(11*12)<1/(11*11)<1/(10*11)
。。。
1/(2014*2015)<1/(2014*2014)<1/(2013*2014)
这样求和实际上就是裂项后销项的处理过程了,
最后设原式=P,有
19*(1/10-1/2015)<P<19*(1/9-1/2014)
通过计算:
1.89<P<2.10
? 好像还确定不了P的整数部分,因为可能为1也可能为2。
看来我们这上边界还大了,需要再缩小。
还是考虑裂项,这么设计会不会更小?
1/(10*10)<1/(9.5*10.5)
1/(11*11)<1/(10.5*11.5)
保持分母两个数间隔1,这么算下来那么
P<19*(1/9.5-1/2014.5)=1.991
那么P<2
所以P的整数部分是 1
答毕。
【5星难度】一道数论题目 a^2-4b和b^2-4a,考验思维
2020/09/11
题目如下:
正整数a,b满足 a2-4b和b2-4a都是完全平方数,问满足条件的a,b有多少组。(如果两组数仅次序不同视为同一组)
据说是浙江某中学数学老师的招聘笔试题,有点难度。
///////////////////////////////////////////////////////////
思考20分钟,
找找思路,
试探一下各种能想到的方法
///////////////////////////////////////////////////////////
这属于数论题,初等数论一般应用的方法有整数除法,同余,奇偶性讨论等。
a2-4b和b2-4a这样的形式是对称的,不妨设 a>=b
讨论:
1、如果a=b
那么a2-4a=n2
即a2-n2-4a=0,进一步
a2-n2-4a+4=4
(a-n-2)(a+n-2)=4(乘积为4,只有1*4, 2*2两种情况,分别讨论)
只有一组解 a=4,b=4
2、如果a>b
我们要思考a、b的关系,a比b大多少?
只有一个条件 a2-4b是一个完全平方数。
我们知道完全平方数有一个特点,即两个相邻的完全平方数之间没有其他完全平方数,
比如25和36之间就不会有其他数是完全平方数。
那么a2-4b和a2之间是否有其他完全平方数?
明显的,a2-4b < a2
a2-4b 会等于(a-1)2吗?
如果a2-4b = (a-1)2
化简上式得到: 2a-4b=1
左边偶数,右边奇数,不能相等
所以 a2-4b < (a-1)2
比 (a-1)2 小的完全平方数就是(a-2)2
所以,我们可以得到
a2-4b <= (a-2)2
化简后,我们有 a - b <=1
因为a-b都是正整数
只能是 a = b + 1
代入 b2-4a= n2
(a-1)2-4a = n2
即 a2-6a+1-n2=0
(a-3-n)(a-3+n)=8
讨论 8=1*8 和 2*4这两种情况,
得到一组解,a = 6, b = 5
因此原题只有两组解,即
a=4,b=4和a=6,b=5
这道题的难点在于确定a和b的关系,同时利用完全平方数的特点,即
两个相邻的完全平方数之间没有其他完全平方数。
再回想一下,
a2-4b是个完全平方数,
a和b只能 a =b 或 a=b+1
这个结论还是很让人震撼的,
这也许就是数学的魅力把~~
