归谬法与直接证明,有n(n≥6)名乒乓球选手进行单循环比赛
2020/10/14
有n(n≥6)名乒乓球选手进行单循环比赛,比赛结果表明:任意5人中既有1人胜其余4人,又有1人负于其余4人,求证:必有1人胜其余n-1人。
///////////////////////////////////////////////////////////
思考20分钟,
找找思路,
试探一下各种能想到的方法,
看看最远能走到哪里
///////////////////////////////////////////////////////////
解析:
因为n不是一个定数,不能通过直接的分类枚举法来证明。
反正法是一种思路,
我们可以假设:没有人胜其余n-1人
假定,胜场最多那个人的编号是1号,
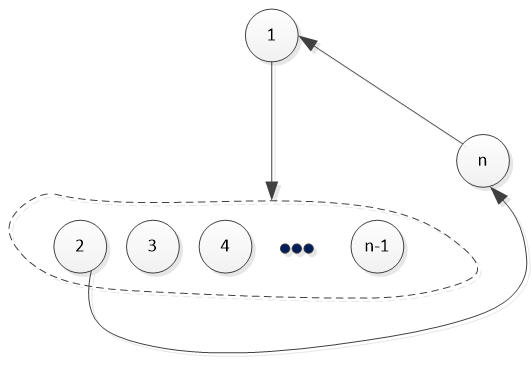
图1
他至少有一人没有胜,设为n,即n打败了1
那么在被1打败的人里面,一定可以找到一个人,比如2号,他打败了n
因为如果没有人能打败n,那么n胜场次就会比1号多1场,与我们的假设矛盾。
所以,此时1、n和2他们的关系是互胜的。
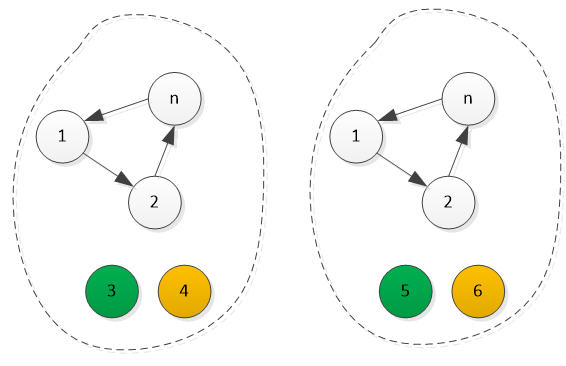
图2
这时我们考虑5人组 1、2、n、3、4
因为1、2、n都有败场,那么全胜的人必定是3或4,我们假定是3全胜,4全败
我们考虑5人组 1、2、n、5、6
那么全胜的人必定是4或5,我们假定是5全胜,6全败
我们考虑5人组 1、2、n、3、5
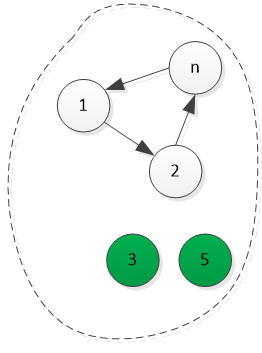
图3
这时我们找不出全败的那个选手,与原题条件矛盾了。
因此我们可以推断,我们的假设错误,
也就间接证明了必有一个人胜其余n-1人。
上面是反正法,我们也可以考虑用直接证明法来试试。
从最小的5个人开始讨论
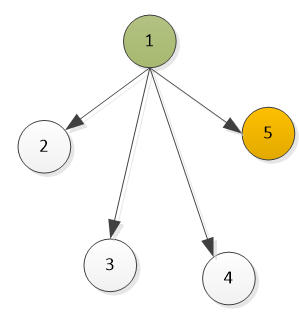
图4
假定有5人,编号为1、2、3、4、5
1胜了其余4人,
现在考虑增加一个6号
讨论1、2、3、4、6这一组
有两种情况:
情况1:如果1胜了6
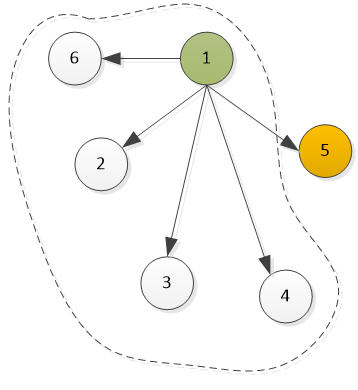
那么1也就胜了2到6的所有人
情况2:如果6胜了1
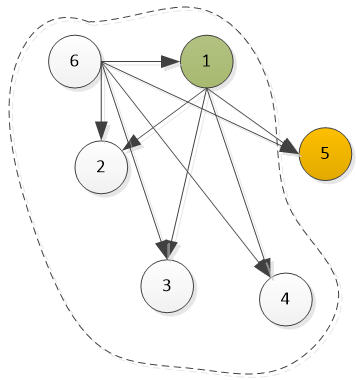
考虑组1、2、3、4、6
因为1胜2、3、4
那么2、3、4不能是全胜的那个,
而1败于6
因此全胜的只能是6号
同样考虑组1、2、3、5、6
6号也必然是全胜的,即6胜5
所以6号胜了所有1到5号
基于上述两种情况的讨论,我们可以找到一个选手(1号或6号),他能全胜。
如果是1号全胜,考虑增加7号,
根据类似的分类讨论,我们也能找到一名全胜的选手,他可能是1号或7号
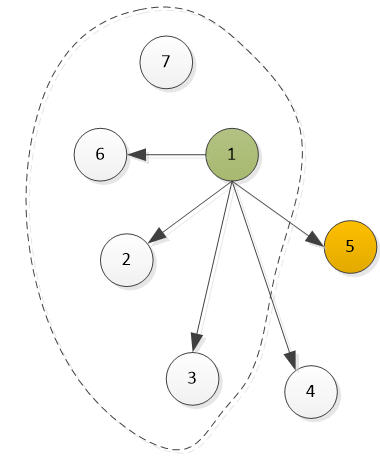
图7
如果是6号全胜,考虑增加7号,
根据类似的分类讨论,我们也能找到一名全胜的选手,他可能是6号或7号
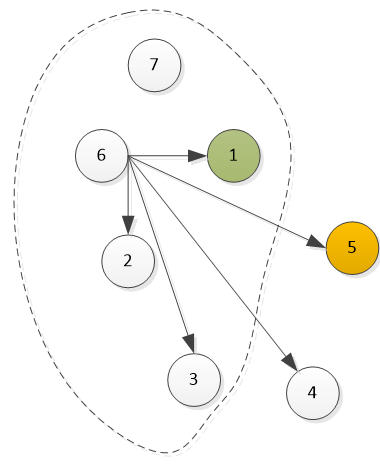
这个过程一直到增加选手n,在他之前,我们可以找到一个选手,胜了所有人,
假定为n-1号
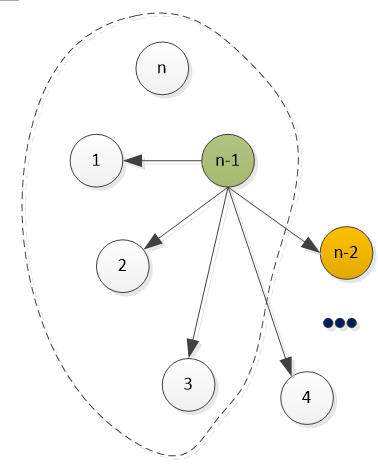
图9
那么n与n-1之间有胜负两种情况:
情况1:n-1胜n,那么n-1就胜了所有人,原题得证
情况2:如果n胜n-1
那么考虑组1、2、3、n-1、n
因为必有1人全胜,1、2、3、n-1都有败场
所以n胜1、2、3
考虑其他组 2、3、4、n-1、n,
同样n胜4
以此类推,n胜n-2
也就是n胜了所有其他人。
原题得证。
点评:
反证法是间接证明,也叫归谬法。在应用的时候,由于多了一个假设,相当于多了个已知条件,自然会好入手一些。但要找出一个并不显而易见的证明仍是一个相当大的智力成就,即便是彻底理解它也需要一定的脑力。
反证法在使用的时候也有一些显而易见的缺点。在聆听或演绎一个证明时,我们不得不自始自终都把我们的注意力集中在一个我们应该要忘记的错误假设上,而不是一条我们应该记住的定理。尤其当反证法这样的证明逻辑很长时,对于听众会很痛苦,我们一个又一个的验证所有的推导过程都正确,但又必须面对全部情况都是不可能的。
对于同一个命题,需要又一点经验才能察觉到直接证明和反证(间接证明)这两者之间并没有本质的对立,两者间也可以进行转化。简而言之,如果我们希望充分的利用自己的能力,就应该熟悉直接和间接两种证明方法,当我们通过一种方法得出一个结论后,也不应该忘记回头再看看这个解答并自问:能否以不同的方式推导出这个结果吗?
