原题如下：
有n（n≥6）名乒乓球选手进行单循环比赛，比赛结果表明：任意5人中既有1人胜其余4人，又有1人负于其余4人，求证：必有1人胜其余n-1人。

///////////////////////////////////////////////////////////
思考20分钟，
找找思路，
试探一下各种能想到的方法，
看看最远能走到哪里
///////////////////////////////////////////////////////////

解析：
因为n不是一个定数，不能通过直接的分类枚举法来证明。
反正法是一种思路，
我们可以假设：没有人胜其余n-1人
假定，胜场最多那个人的编号是1号，

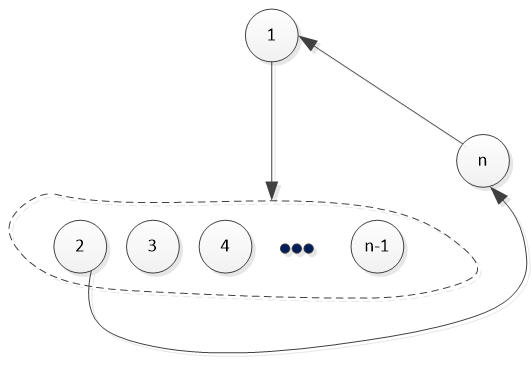
图1

他至少有一人没有胜，设为n，即n打败了1

那么在被1打败的人里面，一定可以找到一个人，比如2号，他打败了n

因为如果没有人能打败n，那么n胜场次就会比1号多1场，与我们的假设矛盾。

所以，此时1、n和2他们的关系是互胜的。

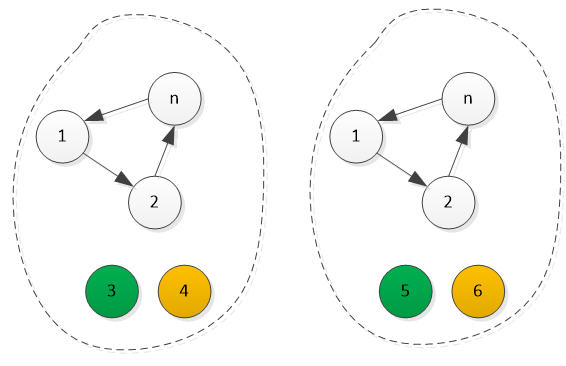
图2

这时我们考虑5人组 1、2、n、3、4

因为1、2、n都有败场，那么全胜的人必定是3或4，我们假定是3全胜，4全败

我们考虑5人组 1、2、n、5、6

那么全胜的人必定是4或5，我们假定是5全胜，6全败

我们考虑5人组 1、2、n、3、5

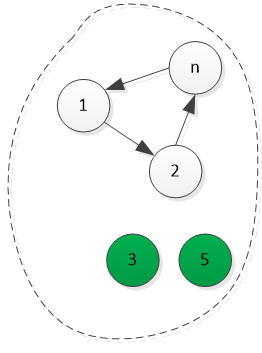
图3

这时我们找不出全败的那个选手，与原题条件矛盾了。
因此我们可以推断，我们的假设错误，
也就间接证明了必有一个人胜其余n-1人。


上面是反正法，我们也可以考虑用直接证明法来试试。
从最小的5个人开始讨论

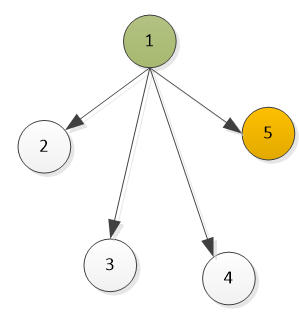
图4

假定有5人，编号为1、2、3、4、5
1胜了其余4人，
现在考虑增加一个6号

讨论1、2、3、4、6这一组
有两种情况：
情况1：如果1胜了6

图5

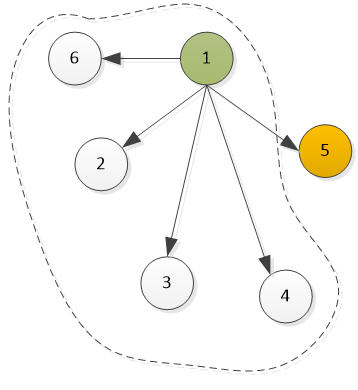
那么1也就胜了2到6的所有人

情况2：如果6胜了1

图6

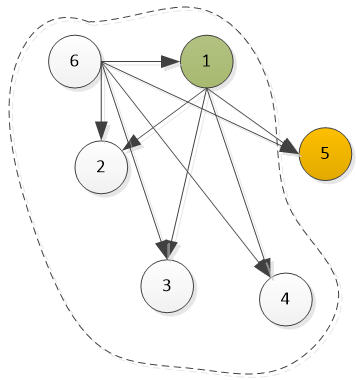
考虑组1、2、3、4、6
因为1胜2、3、4
那么2、3、4不能是全胜的那个，
而1败于6
因此全胜的只能是6号
同样考虑组1、2、3、5、6
6号也必然是全胜的，即6胜5
所以6号胜了所有1到5号

基于上述两种情况的讨论，我们可以找到一个选手（1号或6号），他能全胜。

如果是1号全胜，考虑增加7号，
根据类似的分类讨论，我们也能找到一名全胜的选手，他可能是1号或7号

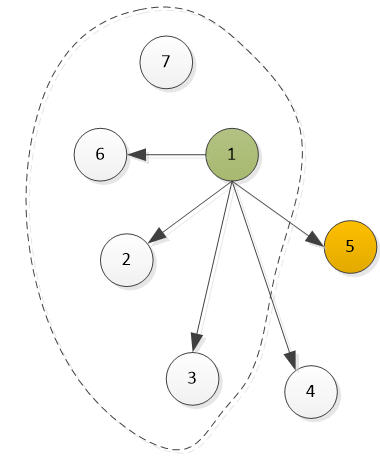
图7

如果是6号全胜，考虑增加7号，
根据类似的分类讨论，我们也能找到一名全胜的选手，他可能是6号或7号

图8

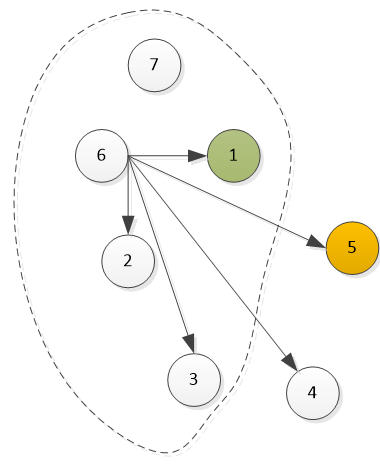
这个过程一直到增加选手n，在他之前，我们可以找到一个选手，胜了所有人，
假定为n-1号

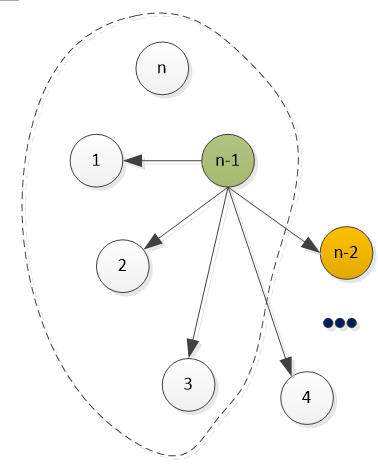
图9

那么n与n-1之间有胜负两种情况：
情况1：n-1胜n，那么n-1就胜了所有人，原题得证
情况2：如果n胜n-1
那么考虑组1、2、3、n-1、n
因为必有1人全胜，1、2、3、n-1都有败场
所以n胜1、2、3
考虑其他组 2、3、4、n-1、n，
同样n胜4
以此类推，n胜n-2
也就是n胜了所有其他人。
原题得证。



点评：
反证法是间接证明，也叫归谬法。在应用的时候，由于多了一个假设，相当于多了个已知条件，自然会好入手一些。但要找出一个并不显而易见的证明仍是一个相当大的智力成就，即便是彻底理解它也需要一定的脑力。

反证法在使用的时候也有一些显而易见的缺点。在聆听或演绎一个证明时，我们不得不自始自终都把我们的注意力集中在一个我们应该要忘记的错误假设上，而不是一条我们应该记住的定理。尤其当反证法这样的证明逻辑很长时，对于听众会很痛苦，我们一个又一个的验证所有的推导过程都正确，但又必须面对全部情况都是不可能的。

对于同一个命题，需要又一点经验才能察觉到直接证明和反证（间接证明）这两者之间并没有本质的对立，两者间也可以进行转化。简而言之，如果我们希望充分的利用自己的能力，就应该熟悉直接和间接两种证明方法，当我们通过一种方法得出一个结论后，也不应该忘记回头再看看这个解答并自问：能否以不同的方式推导出这个结果吗？

青海的草原，一眼看不完；
喜瑪拉雅山，峰峰相連到天邊。
古聖和先賢，在這裡建家園；
風吹雨打中，聳立五千年。

原题如下：

有若干把锁，现有6个人各掌握了其中一部分锁的钥匙，已知任意2人同时去开锁，恰好有一把锁打不开，而任意三个人都可以把全部锁打开。那么至少有几把锁。

 

///////////////////////////////////////////////////////////
思考20分钟，
找找思路，
试探一下各种能想到的方法
///////////////////////////////////////////////////////////

 

 

解析：

这道题属于最值问题，需要我们构造论证。

但如果一上来就开始构造，会浪费很多时间。

我们要分析原题带来的限制条件。

设锁为1、2、3、。。。n

6个人分别为P1、P2、P3、P4、P5、P6

 

首先考虑“已知任意2人同时去开锁，恰好有一把锁打不开”。

这里有6个人，任意两人的组合有C(6,2)=15种

在这15种组合中，我们要问一个问题：是否有两种组合它们打不开的锁相同？

如有相同，比如P1+P2和P3+P4都开不了锁1，

那么也就是P1+P2+P3+P4这4个人一起都打不开锁1，

这和原题中第二个条件矛盾了，即“任意三个人都可以把全部锁打开”。

所以，我们可以得到：

这15种组合中，打不开的锁都互不相同

也就是说锁的个数n>=15

 

我们讨论n=15的情况。

假设P1+P2缺第k把钥匙，那么k一定在P3、P4、P5、P6手中，

因为“任意三个人都可以把全部锁打开”

同样，对于任意一把钥匙k，有且只有4个人有。

每把锁有且仅有4把同样的钥匙，

这样我们可以计算每个人有几把钥匙：

15x4/6=10（把）

 

进过上述讨论，我们知道锁有15把，每个人有钥匙10把，我们尝试构造。

我们知道每两个人都缺一把钥匙，可以列表表示如下：

组合	缺钥匙编号
P1+P2	1
P1+P3	2
P1+P4	3
P1+P5	4
P1+P6	5
P2+P3	6
P2+P4	7
P2+P5	8
P2+P6	9
P3+P4	10
P3+P5	11
P3+P6	12
P4+P5	13
P4+P6	14
P5+P6	15

根据以上缺钥匙编号的假定，我们可以构造出每个人拥有钥匙的情况：

组合	缺少钥匙编号	拥有钥匙编号
P1	1、2、3、4、5	6 7 8 9 10 11 12 13 14 15
P2	1、6、7、8、9	2 3 4 5 10 11 12 13 14 15
P3	2、6、10、11、12	1 3 4 5 7 8 9 13 14 15
P4	3、7、10、13、14	1 2 4 5 6 8 9 11 12 15
P5	4、8、11、13、15	1 2 3 5 6 7 9 10 12 14
P6	5、9、12、14、15	1 2 3 4 6 7 8 10 11 13

点评：

本题是需要先证明后构造的逻辑推理题，与前几天的那道连续自然数数码和不是16倍数的那道题刚好相反。这类题是近年以来数学竞赛的热点，要求我们不仅要善于观察和思考，还要敢于猜测和联想。

原题如下：

最多有多少个连续的自然数，它们的各位数字和都不是5的倍数？

 

//////////////////////////////////////////////////

思考过程：

先举一个例子，如

1、2、3、4、5、6、7、8、9、10、11、12、13、14、15

这一串数，它们的各位数字和分别为：

1、2、3、4、5、6、7、8、9、1、2、3、4、5、6

因为，这些数要求是连续的自然数，那么后一个自然数一定比在它前面的自然数大1

如果它们除了个位数以外的数字都相同，那么它们的数字和也将是一些相邻的自然数，

比如这里的

10、11、12、13、14、16

它们的十位相同仅个位数不同，其各位数字和分别是：

1、2、3、4、5、6

是一串连续的自然数。

数串8、9、10、11、12就不符合这个规律，因为它们十位不同。

 

我们还知道，

任何连续的5个自然数必然有一个能被5整除

因为5各连续自然数除以5的余数只能有1、2、3、4和0 这5种情况

 

考虑原题的要求，我们猜测：

仅个位数不同的自然数串最多连续有4个，其数码和不是5的倍数

另外在加上十位数与上述不同的连续4个，

总共是8个

比如 6、7、8、9、10、11、12、13

 

对于上述猜想，我们需要严格证明。

要证明最多是8个，自然想到9个可不可以，或者比8个多是否可行？这是反证法，也就是归谬法。如果超过8个不可以，同时我们又能构造出8个连续自然数的一个例子，那么也就完成了证明。思路是这样，考虑如何入手。

 

设有一串自然数，个数大于等于9个。根据前面的讨论，我们知道

1、如果它们除了个位数以外的数字都相同，那么它们的数字和也将是一些相邻的自然数

2、任何连续的5个自然数必然有一个能被5整除

能想到什么？这9个数有可能除了个位数以外的数字都相同，也有可能十位数不同。

按照十位数以上数字是否相同，我们把这9个数分为两类，根据抽屉原理，必然有一类数字个数大于等于5个，那么这5个数，它们的各位数码和就是连续的5个自然数，也就是有必能被5整除的一个数。

 

这样就证明了前面的猜想。

所以本题的答案是8

 

 

这类问题，还有升级版，题目如下：

最多有多少个连续的自然数，它们的各位数字和都不是16的倍数？

 

解析：

最小的两位数79其数字和等于16，也就是从1开始直到78，

这78个自然数其数码和都不是16的倍数。

那么78是最多的满足条件的连续自然数个数吗？

 

类似第一道题的考虑方式，按百位以上数字是否相同我们把目标的这串数分为两段，

后一段从1000….00（K个0），开始直到1000…0068（K个0），

最后两位数字不能超过68，因为1+6+9=16了

前一段应该从999….开始到999…99（K个9）

 

接着分析，

00、01、02直到68，这两位数码和是0到14，共15个，没有其他了

从31、32、33直到99，这两位数码和是4到18，共15个，也没有其它了

这样最好了，我们目标就要构造这样的数列。

因为如果有16个数码和，则必然有一个能被16整除（抽屉原理）

继续构造第一个数99..31

31前面有n个9

目标：9*n + 4除16余1

n=5满足

即9999931直到9999999这69个数的数码和除16的余数只能是1到15之间的任意数，

不会有数的数码和被16整除

 

所以9999931到10000068这138个数的数码和不能被16整除。

 

是否138就是最大呢？

这里的证明需要用到抽屉原理，

即把大于等于139个连续的自然数，按百位以上数码是否相同分成两部分，其中一部分必然大于等于70个。

假设：

1、大于70个数的那一组最大的百十位数为99

那么这一组最小数必然小于等于30，

其数码和从3到18，共16个，包括16，根据抽屉原理

不论其百位以上数码和是多少，这一组数中必有一个数的数码和能被16整除。

 

2、大于70个数的那一组最小的百十位数位00

那么这一组最大数必然大于等于69，

其数码和从0到15，共16个，包括16，根据抽屉原理

不论其百位以上数码和是多少，这一组数中必有一个数的数码和能被16整除。

 

也就是说，138是最大的自然数数串的数字个数。

点评：

第一题虽然简单，其实我们也用了构造。从简单的数列构造中，探寻约束条件下的规律。

第二题，如果没有构造目标数列，我们不能直接想到70个连续自然数的数串的性质，也就不能应用抽屉原理来进一步证明。在构造的过程中，我们也应用了抽屉原理。抽屉原理本身也是一种抽象的构造技巧，即我们要设计抽屉，也要设计苹果。

在解题的很多时候，我们要经常想一想，是否有做过类似的题，这个难题的简化版本是什么。

从简单入手，套用熟悉的模型，往往是一个解决复杂问题的有效办法。

昨天在听网络频道的时候，了解到一个圣经故事，觉得比较有启发性，后来详细查看了故事的一些细节，摘录如下。

 

约翰福音8:1-11

8:1 于是各人都回家去了，耶稣却往橄榄山去。

8:2 清早又回到殿里，众百姓都到他那里去，他就坐下教训他们。

8:3 文士和法利赛人带着一个行淫时被拿的妇人来，叫她站在当中。

8:4 就对耶稣说：“夫子，这妇人是正行淫之时被拿的。

8:5 摩西在律法上吩咐我们，把这样的妇人用石头打死。你说该把她怎么样呢？”8:6 他们说这话，乃试探耶稣，要得着告他的把柄。耶稣却弯着腰用指头在地上画字。

8:7 他们还是不住地问他，耶稣就直起腰来，对他们说：“你们中间谁是没有罪的，谁就可以先拿石头打她。”

8:8 于是又弯着腰用指头在地上画字。

8:9 他们听见这话，就从老到少一个一个地都出去了，只剩下耶稣一人，还有那妇人仍然站在当中。

8:10 耶稣就直起腰来，对她说：“妇人，那些人在哪里呢？没有人定你的罪吗？”

8:11 她说：“主啊，没有。”耶稣说：“我也不定你的罪，去吧！从此不要再犯罪了。”

 

对这个故事，读来有几点体会。

首先，每个人都是有罪的，每个人参与社会生活，不可能不做错事。每个人都应该对自己的罪过进行忏悔。但一般世人，通常只看见别人的过错，而看不见自己的过错。

其次，应该学会宽恕别人，不可律人以严，待己以宽。你我都是罪人。罪人没有资格定罪人的罪。在定他人罪时，先思考自己是否无罪。法官法第十条规定曾因犯罪受过刑事处罚的不得担任法官，所以现代也是认同不犯罪的人才有资格审判他人的。

第三，保持清醒的头脑，用智慧去解决问题

当时的背景是耶稣正在圣殿中教训人，受到法利赛人的试探，法利赛人把行淫时被捉的女人带到耶稣面前，让耶稣作决断要不要遵照摩西的律法治死这个女人，好拿他的把柄。他们所问的问题实际是一个陷阱，意图使主耶稣陷在一个进退两难的境地，因为无论主耶稣怎样回答，总会让他们有控告他的把柄。如果耶稣建议饶恕这妇人，他们就会指控他不肯主持公义，触犯了摩西的律法；但如果耶稣主张照摩西的律法把妇人处死，他们也会指控他触犯了罗马帝国的民法，因为当时罗马政府并未授予犹太人杀人的权柄。此外，这种不怜悯人的态度，也违反了基督“救赎主”的使命。

耶稣清楚他们的伎俩，故意弯着腰在地上写字。在众人的一再追问下，耶稣回答，“你们中间谁是没有罪的，谁就可以先拿石头打她。”这个回答非常有智慧，通过假定逻辑，实际上把问题还给了出问题的人。这种方式在我们进行各种谈判或高难度对话，值得借鉴。

最后众人的离开是各自良心发现还是阴谋无法得逞而败落呢？我觉得是后者。因为，按照当时犹太律法规定，因行淫被处罚的人，应该是两个即男女双方，而文士和法利赛人只带来了其中的一个。当时的情况很可能是，这个妇人是遭到了不合法的逮捕。而犹太人如果直接把她打死，那么根据罗马法律，他们都犯了谋杀罪。也就是说，这些人其实并没有处死这个女人的权力。他们不在乎这个女人到底应不应该受惩罚。恶毒的想将耶稣置于教唆谋杀的罪名中，这才是目的。

所以，耶稣的回答不但避免了被质疑违反犹太律法，也避免了违反罗马法律，还拯救这个女人脱离了非法的惩罚。

对于此事，耶稣不做评论或者建议他们寻求罗马地方执政官处理如何？文士和法利赛人的询问把耶稣陷入窘境里，他们称呼耶稣为“夫子”，换言之，耶稣不能回避他们所提的问题，因为他们把他当作律法的教师，向他询问律法的问题。耶稣置之不理或错误解释都会减少群众对他的信赖。

 

这是一个关于罪、宽恕和智慧的故事，有感于斯文，特著文以记之。

甲乙两个人手上各有一些牌，具体如下：
甲： 一对A  一对10 
乙:  红心 3 、5 、9 、Q 、2
     黑桃  4 、6  、7 、J 、Q 
     梅花  4 、6 、9 、J 
     方片  5 、7 、J 、Q

规则：
不许出连对、三个不可以带牌 
可以出顺子、同花（5张同色一起出）
谁先出完谁胜

乙先出，乙是否能赢？

///////////////////////////////////////////////////////////

对于乙，

黑桃的5张可以出同花，

红心3、5，梅花4、6方片7可以出顺子

剩下，5、2，99 JJ和QQ

这个时候，出方片5

如果：

1、甲不要，乙则继续打单，直到全部出完

2、甲要，出10

乙出J，

甲出A，那么乙出2，乙还有两个对一个J，继续出完，乙赢

甲不出A，乙继续出单个J，甲继续不出，乙出单个Q，

甲还是不能出A，因为出A后，甲剩下10、A，乙剩下2、99、Q，乙能出完

最后甲两个A只能拿在手里憋死了。

结论是乙可以赢